The Gauss-Seidel method is an iterative technique used to solve linear systems of equations. It is a numerical method that can be used to find a solution to a system of linear equations, and it has many applications in mathematics and engineering. In this blog post, we’ll take a look at what the Gauss-Seidel method is, as well as how it works and why it’s so useful.
What Is the Gauss-Seidel Method?
The Gauss-Seidel method is a numerical technique used to solve systems of linear equations. It works by taking each equation in the system one at a time, starting with the first equation, and then solving for the unknowns using simple algebraic techniques. This process is repeated until all unknowns have been solved or until no further progress can be made. The method is similar to the Jacobi method, but it uses the values of the variables from the previous iteration to update the values in the current iteration. This can sometimes lead to faster convergence compared to the Jacobi method.
How Does the Gauss-Seidel Method Work?
The Gauss-Seidel method works by taking each equation in the system one at a time. We start with the first equation and solve for any unknowns using simple algebraic techniques. Once we’ve solved all unknowns on that equation, we move on to the next equation and repeat this process until all unknowns have been solved or until no further progress can be made. For example, let’s say we have three equations with three unknowns (x1, x2, x3):
6×1 + 2×2 – 5×3 = -7
3×1 + 4×2 – 2×3 = 8
5×1 + 7×2 – 3×3 = 0
We would start by solving for x1 on the first equation (6×1 + 2×2 – 5×3 = -7). We use simple algebraic techniques to solve for x1 on this equation (e.g., subtracting 6 from both sides of the equation). Once we’ve solved for x1 on this equation, we move on to solving for x2 on this same equation (i.e., 2×2 – 5×3 = -13). We repeat this process until all unknowns have been solved or until no further progress can be made. Once all unknowns are solved for or no more progress can be made with one equation, we move on to the next equation in our system and repeat this same process until all equations have been exhausted or no further progress can be made overall.
The Gauss-Seidel method is typically used when the coefficient matrix is diagonally dominant, meaning that the absolute value of the diagonal element is greater than the sum of the absolute values of the other elements in the same row. This condition helps to ensure the convergence of the method.
Gauss Seidel Method MATLAB Code Download
Here is a sample Gauss-Seidel load flow program in MATLAB:
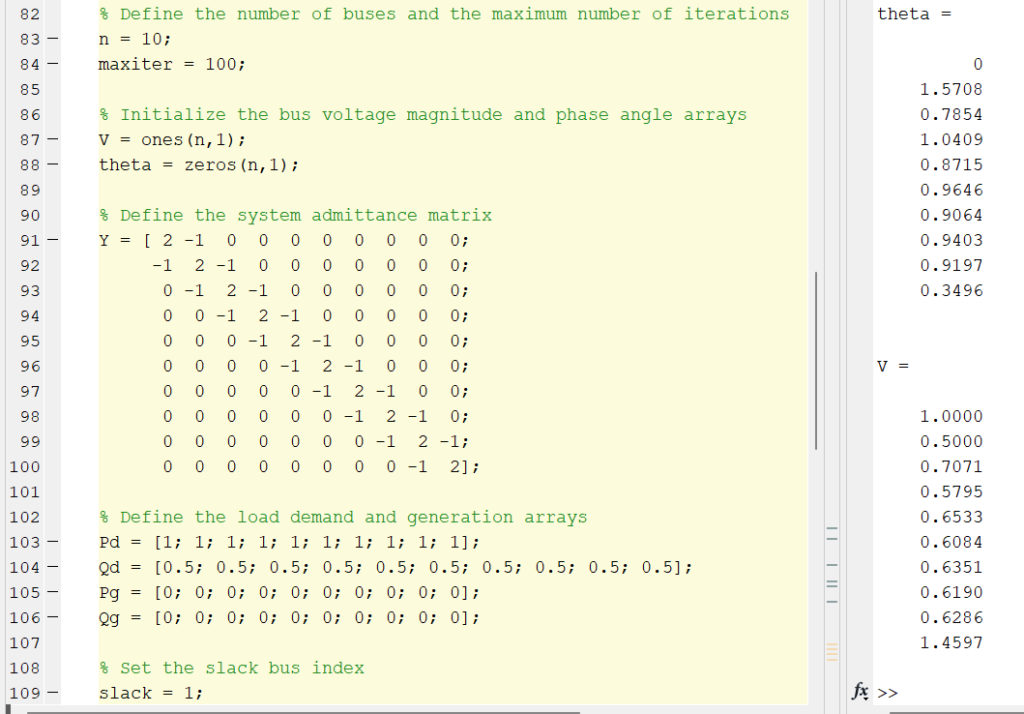
% Define the number of buses and the maximum number of iterations
n = 10;
maxiter = 100;
% Initialize the bus voltage magnitude and phase angle arrays
V = ones(n,1);
theta = zeros(n,1);
% Define the system admittance matrix
Y = [ 2 -1 0 0 0 0 0 0 0 0;
-1 2 -1 0 0 0 0 0 0 0;
0 -1 2 -1 0 0 0 0 0 0;
0 0 -1 2 -1 0 0 0 0 0;
0 0 0 -1 2 -1 0 0 0 0;
0 0 0 0 -1 2 -1 0 0 0;
0 0 0 0 0 -1 2 -1 0 0;
0 0 0 0 0 0 -1 2 -1 0;
0 0 0 0 0 0 0 -1 2 -1;
0 0 0 0 0 0 0 0 -1 2];
% Define the load demand and generation arrays
Pd = [1; 1; 1; 1; 1; 1; 1; 1; 1; 1];
Qd = [0.5; 0.5; 0.5; 0.5; 0.5; 0.5; 0.5; 0.5; 0.5; 0.5];
Pg = [0; 0; 0; 0; 0; 0; 0; 0; 0; 0];
Qg = [0; 0; 0; 0; 0; 0; 0; 0; 0; 0];
% Set the slack bus index
slack = 1;
% Set the tolerance for convergence
tol = 1e-6;
% Initialize the iteration counter
iter = 0;
% Iterate until convergence or maximum number of iterations reached
while iter < maxiter
% Increment the iteration counter
iter = iter + 1;
% Initialize the error sum
err = 0;
% Loop through all buses
for i = 1:n
% Skip the slack bus
if i == slack
continue;
end
% Compute the sum of active and reactive power injections
S = V(i) * (Y(i,:) * V) + 1j * (Qd(i) - Qg(i));
% Solve for the bus voltage magnitude and phase angle
V(i) = abs(S) / (Pd(i) - Pg(i));
theta(i) = angle(S) + angle(V(i));
% Update the error sum
err = err + abs(V(i) - abs(S) / (Pd(i) - Pg(i)));
end
% Check for convergence
if err < tol
break;
end
end
Gauss-seidel method MATLAB code used to solve distribution system load flow problem is available for download. The code provides a simple implementation of the iterative method as described above and can be used to solve linear systems of equations.
How to Define System Admittance Matrix in MATLAB
This is a symmetric matrix with 10 rows and 10 columns, representing a power system with 10 buses. The elements of the matrix represent the mutual admittances between the buses. For example, the element Y(2,1) represents the mutual admittance between bus 2 and bus 1, and the element Y(1,2) represents the mutual admittance between bus 1 and bus 2. The diagonal elements of the matrix represent the self-admittances of the buses.
The values of the admittance matrix elements can be obtained from the network data, such as the line impedances and the transformer parameters. The values may also be modified to account for line charging and shunt elements such as capacitors and reactors.
Y = [ 2 -1 0 0 0 0 0 0 0 0; -1 2 -1 0 0 0 0 0 0 0; 0 -1 2 -1 0 0 0 0 0 0; 0 0 -1 2 -1 0 0 0 0 0; 0 0 0 -1 2 -1 0 0 0 0; 0 0 0 0 -1 2 -1 0 0 0; 0 0 0 0 0 -1 2 -1 0 0; 0 0 0 0 0 0 -1 2 -1 0; 0 0 0 0 0 0 0 -1 2 -1; 0 0 0 0 0 0 0 0 -1 2];
Why Is It Useful?
The Gauss–Seidel method is useful because it allows us to quickly approximate solutions to systems of linear equations without having to use complex mathematical techniques such as matrix inversion or other more difficult algorithms like Newton’s method or gradient descent optimization methods. Additionally, it’s often faster than other methods since it only requires solving one variable at a time instead of having to consider multiple variables simultaneously (as is required with other methods). Finally, it’s also relatively easy to implement since its steps are very straightforward and intuitive—making it an ideal choice when speed and ease of implementation are important considerations.
When is it best to use the Gauss-Seidel Method, and when should another method be used instead?
Several load flow methods are faster and more accurate than the Gauss-Seidel method. Some examples include the Newton-Raphson method, fast decouple, and the Backward/Forward sweep load flow method.
The Newton-Raphson method is a widely used method for solving load flow problems in power systems. It is an extension of the Gauss-Seidel method that uses Newton’s method to linearize the nonlinear equations of the power system and solve them iteratively. The Newton-Raphson method can converge faster than the Gauss-Seidel method and is more accurate, especially for systems with large or highly interconnected networks.
The fast decoupling method is another iterative method that is used to solve load flow problems in power systems. It is based on the Newton-Raphson method and uses an approximation of the Jacobian matrix to decouple the load flow equations into two sets of equations that can be solved independently. This allows the method to converge faster than the Newton-Raphson method for some systems.
In general, the choice of load flow method depends on the specific characteristics of the power system being analyzed and the desired level of accuracy and computational efficiency.
Conclusion
The Gauss–Seidel method is an iterative technique used to solve linear systems of equations quickly and easily without having to use complex mathematical techniques such as matrix inversion or other more difficult algorithms like Newton’s method or gradient descent optimization methods. It’s often faster than other methods since it only requires solving one variable at a time instead of having to consider multiple variables simultaneously which makes implementing it relatively easy compared to other options available too! Ultimately if you need an efficient way of solving your linear equations then considering using the Gauss–Seidel method should be something worth looking into!
