Algebra is one of the most important branches of mathematics, and it can be a powerful tool for problem-solving. In algebra, equations are used to express relationships between variables. There are several different types of equations that each has its unique uses and properties. Understanding these different types of equations will allow you to use algebra more effectively when solving problems. This article will demystify the various kinds of algebraic equations, from linear equations to quadratic ones, so you can better understand how they work and apply them in your problem-solving endeavors.
How Algebraic Equations Playing Role in Mathematics, Science, and Engineering
Algebraic equations are an essential part of mathematics, and they play a crucial role in many areas of science, engineering, and technology. They are used to model and analyze a wide range of physical, biological, and social phenomena, and they provide a powerful tool for understanding and solving problems.
In mathematics, algebraic equations are used to describe and solve problems involving variables and unknowns. Algebraic equations are used to model mathematical relationships, and they allow us to express mathematical problems in a compact and convenient form. They also allow us to make predictions and test hypotheses, and they are used to find solutions to problems involving optimization, probability, and statistics.
In science and engineering, algebraic equations are used to model and analyze physical systems, such as mechanical, electrical, and chemical systems. They are used to describe the behavior of these systems, and they are used to predict how the systems will behave under different conditions. They also play a key role in the design and analysis of control systems, and they are used to optimize the performance of these systems.
In addition, algebraic equations are also important in load flow analysis, computer science, and other related fields. They are used to model algorithms, and data structures and to solve optimization problems.
In summary, algebraic equations are an important tool in mathematics, science, and engineering, and they play a key role in many areas of research and technology. Understanding how to work with and solve algebraic equations is essential for success in these fields, and for solving real-world problems.
What are the Different Types of Algebraic Equations
There are many types of equations in mathematics, and they can be broadly classified into several categories based on their characteristics such as the degree of the equation, the types of operations involved, the number of solutions, and the type of function they represent.
It’s difficult to give an exact number because equations can be transformed and manipulated to fit into different categories and new types of equations are being discovered and studied constantly.
However, Some common types of equations include:
- Linear equations
- Quadratic equations
- Cubic equations
- Polynomial equations
- Radical equations
- Rational equations
- Exponential equations
- Logarithmic equations
- Trigonometric equations
- Systems of equations
- Differential equations
- Integral equations
- Partial differential equations
These are just some examples of the types of equations that exist in mathematics, but many others exist, including those in fields such as complex analysis, abstract algebra, number theory, and more. Additionally, as new equations and new types of equations are being studied, the list may change over time.
In algebra, several types of equations can be classified based on the number of solutions they have, the degree of the equation, and the type of operations involved. Some common types of equations include:
Linear equations
Linear equations are equations that can be written in the form ax + b = 0, where a and b are constants and x is the variable. Linear equations have a degree of one, and the graph of a linear equation is a straight line. These equations have one solution, which can be found by using simple algebraic techniques, such as the addition or subtraction of equations or division. Linear equations are used to model a wide range of physical and mathematical systems, including simple harmonic motion, electrical circuits, and geometric shapes.
Example: 2x + 5 = 0
To solve this equation, we first want to get the variable x alone on one side of the equation. To do this, we can subtract 5 from both sides of the equation:
2x + 5 = 0
2x = -5
Next, we can divide both sides of the equation by 2 to find the value of x:
2x = -5
x = -5/2
So the solution to this linear equation is x = -5/2.
It’s important to note that to solve a linear equation, we must first simplify the equation by combining like terms, if any, then isolating the variable on one side of the equation, and finally, applying any mathematical operations required to find the value of the variable.
This is one example of a linear equation, there are many other ways to represent and write a linear equation, but the process of solving is the same.
Quadratic equations
Quadratic equations are equations that can be written in the form of ax^2 + bx + c = 0, where a, b and c are constants, and x is the variable. These equations have a degree of two and they can have one, two, or no solutions. Quadratic equations are used in physics, engineering, and other sciences to model a wide range of phenomena that follow a parabolic or inverted parabolic path such as the motion of projectiles and oscillations.
Factoring
We can factor the left side of the equation by finding two numbers that multiply to -4 and add to -3. These numbers are -4 and 1. So we can factor the left side of the equation as (x-4)(x+1) = 0. Now we can set each factor equal to zero and solve for x.
x-4 = 0 or x+1 = 0
x = 4 or x = -1
Quadratic Formula
The solution of the equation can be found by using the quadratic formula. The quadratic formula is:
x = (-b ± √(b^2 – 4ac))/2a
where a, b and c are the coefficients of the equation.
x = (-(-3) ± √((-3)^2 – 41(-4)))/2*1
x = (3 ± √(9 + 16))/2
x = (3 ± √25)/2
x = (3 ± 5)/2
x = 8/2 or x = -2/2
x = 4 or x = -1
Completing the square
We can complete the square by adding and subtracting the square of half of the coefficient of x squared.
(x^2 – 3x) + 3/2^2 – 3/2^2 = 0
x^2 – 3x + 9/4 = 0
(x-3/2)^2 = 9/4
x = 3/2 ± √9/4
x = 3/2 ± 3/2
x = 3 or x = -1/2
So the solutions to this quadratic equation are x = 4 or x = -1.
It’s important to note that different methods of solving a quadratic equation may yield different results, but the solutions must be checked to make sure that they are valid solutions for the given equation.
Cubic equations
Equations that can be written in the form of ax^3 + bx^2 + cx + d = 0, where a, b, c, and d are constants, and x is the variable. These equations have a degree of three and can have one, two, or three solutions. Solving a cubic equation can be more complex than solving a linear or quadratic equation. There are different methods to solve a cubic equation, such as factoring, using the cubic formula, using trigonometric substitution, or using numerical methods. Here is an example of a cubic equation and its solution using the cubic formula:
Example: x^3 + 3x^2 – 7x – 5 = 0
To solve this equation, we can use the cubic formula, which is a formula that gives the solutions of a cubic equation in terms of its coefficients. The cubic formula is:
x = (-b + √(b^2 – 4ac) + √(3a^2b^2 – 4a^3c – 4b^3c + 18abc – 27a^2d – 27b^2d + 4ac^2))^(1/3) + (-b – √(b^2 – 4ac) + √(3a^2b^2 – 4a^3c – 4b^3c + 18abc – 27a^2d – 27b^2d + 4ac^2))^(1/3)
where a, b, c, and d are the coefficients of the equation.
x = (-3 + √(3^2 – 41(-7) – 41(-5)) + √(3*1
Polynomial equations
Equations that involve multiple powers of x and constants. They can have any degree, and the number of solutions depends on the degree of the equation and the number of real or complex roots.
Example: x^4 – 6x^3 + 11x^2 – 6x + 1 = 0
One method to solve this equation is by factoring the polynomial.
Solution:
First, we can factor out a common factor of x^2 – x + 1 from the equation:
x^4 – 6x^3 + 11x^2 – 6x + 1 = (x^2 – x + 1)(x^2 – 5x + 1) = 0
Now we can set each factor equal to zero and solve for x:
x^2 – x + 1 = 0 or x^2 – 5x + 1 = 0
We can then solve for x by factoring the quadratic equations:
(x-1)^2 = 0 or (x-1)(x-1) = 0
x-1 = 0
x = 1
or
(x-1)(x-5) = 0
x-1 = 0 or x-5 = 0
x = 1 or x = 5
So the solutions of this polynomial equation are x = 1 and x = 5.
It’s important to note that this is only one way to solve a polynomial equation, and depending on the complexity of the equation and the degree of the polynomial, other methods such as synthetic division, long division, or the Rational Root Theorem could be used.
Radical equations
Equations that involve a root or a power of x, such as square roots, cube roots, etc. They can be hard to figure out, but when you do it can tell you something about your problem. For example, if you have a problem that involves taking the square root of something, then this type of equation can tell you how to solve it.
Example: √(x+4) = x
To solve this equation, we can first square both sides to eliminate the square root:
x+4 = x^2
Then we can move all the terms to one side of the equation:
x^2 – x – 4 = 0
Now we can factor this equation:
(x-4)(x+1) = 0
From this step, we can find the roots of the equation by setting each factor equal to 0 and solving for x:
x-4 = 0 or x+1 = 0
x = 4 or x = -1
So the solutions of this radical equation are x = 4 or x = -1
It’s important to note that in this example, squaring both sides of the equation didn’t change the solution because the equation was already true and it is true for the solutions we found. However, this is not always the case, squaring both sides can lead to extraneous solutions, it is important to check the solutions found by solving the original equation.
Rational equations
Equations that involve fractions of x and constants. The number of solutions depends on the degree of the equation and the number of real or complex roots.
Example: (2x-3) / (x^2-4x+4) = 3
To solve this equation, we can first multiply both sides by the denominator to clear the fractions:
2x-3 = 3x^2-12x+12
Then we can move all the terms to one side of the equation:
3x^2-14x+15=0
Now we can factor this equation:
(3x-5)(x-3) = 0
From this step, we can find the roots of the equation by setting each factor equal to 0 and solving for x:
3x-5 = 0 or x-3 = 0
x = 5/3 or x = 3
So the solutions of this rational equation are x = 5/3 or x = 3
It’s important to note that in this example, the denominator of the original equation was a factorable quadratic equation and that’s why we were able to find the solutions by factoring, but in some cases, the denominator can be a more complex polynomial equation, in that scenario we may need to use other methods to find the solutions such as long division, synthetic division or graph the equation to find the solutions.
Exponential equations
Equations that involve exponential functions such as e^x are used in many different fields and applications. In mathematics, they are used to model population growth, radioactive decay, and chemical reactions. In physics, they are used to describe wave motion, light propagation, thermodynamic processes, and more.
Example: 2^x = 8
To solve this equation, we can first take the logarithm of both sides with base 2:
x = log2(8)
The logarithm of 8 with base 2 is equal to 3, therefore:
x = 3
So the solution of this exponential equation is x = 3.
It’s important to note that the logarithm of a number with base b is defined as the exponent that we need to raise b to get that number. In this case, we know that 2^3 = 8, so the logarithm base 2 of 8 is 3.
Also, there are other types of exponential equations such as logarithmic equations, in that case, we can use properties of logarithms to simplify the equation and find the solution.
Logarithmic equations
Equations that involve logarithmic functions are equations in which a quantity is expressed as the logarithm of another quantity.
Trigonometric equations: Equations involving trigonometric functions such as sine, cosine, and tangent.
Example: log2(x) = 3
To solve this equation, we can first raise 2 to the power of 3 on both sides of the equation:
2^3 = x
Then we can simplify the right side of the equation:
8 = x
So the solution of this logarithmic equation is x = 8.
It’s important to note that the logarithm of a number with base b is defined as the exponent that we need to raise b to get that number. In this case, we know that log2(8) = 3, so the x has to be 8.
Also, there are other types of logarithmic equations, for example, logarithmic equations with different bases, in that case, we can use logarithmic properties such as logarithms with different bases to find the solution.
Differential equations
A differential equation is an equation involving an unknown function and its derivatives. These equations express the relationship between the derivatives of a function and the function itself. For example, the equation dy/dx = x^2 is a first-order differential equation, where y is the unknown function and x is the independent variable. Differential equations are used to model a wide range of physical systems, including mechanical systems, electrical systems, and biological systems.
Example: dy/dx + 2y = x^2
A differential equation is an equation that relates a function and its derivatives. In this example, y is the function and dy/dx represents its derivative concerning x. This is a first-order, linear differential equation, which means that it involves only the first derivative of y and the independent variable is x.
One method to solve this differential equation is by using an integrating factor. An integrating factor is a technique that allows us to transform a non-exact differential equation into an exact one.
Solution:
- Find an integrating factor I(x) for the differential equation. In this case, we can use I(x) = e^(2x)
- Multiply both sides of the differential equation by I(x), and we get:
e^(2x) dy/dx + 2e^(2x) y = e^(2x) x^2
- Now we can integrate both sides of the equation concerning x
∫ e^(2x) dy/dx dx = ∫ e^(2x) x^2 dx + C
- we can solve the left side of the equation and we get:
e^(2x) y = ∫ e^(2x) x^2 dx + C
- Solve the integral on the right side of the equation to get:
e^(2x) y = (1/3) e^(2x) x^3 + C
- Now we can divide both sides of the equation by e^(2x) to find y
y = (1/3) x^3 + C/e^(2x)
The solution is y = (1/3) x^3 + C/e^(2x) where C is an arbitrary constant.
This is a general solution for this differential equation, C is an arbitrary constant that can be determined by initial or boundary conditions.
It’s important to note that there are different methods to solve differential equations, and the method used to solve a differential equation will depend on the specific form of the equation. For example separation of variables, substitution, or series solutions.
Integral equations
An integral equation is an equation in which an unknown function appears under an integral sign. Integral equations relate the integral of a function over a region to the function itself. They are used to model a wide range of systems, including heat conduction, fluid flow, and electromagnetic systems.
Sure, here is an example of an integral equation and its solution:
Example: y(x) = x + ∫_0^x (2y(t)+1) dt
An integral equation is an equation that relates a function and an integral of that function. In this example, y(x) is the unknown function, and the integral on the right side of the equation is taken concerning t from 0 to x.
One method to solve this integral equation is by using the method of successive approximations. This method involves iteratively approximating the solution by using a known function that serves as an initial guess for the true solution.
Solution:
- Make an initial guess for the solution y0(x) = x
- Substitute the initial guess into the integral equation to get a new function: y1(x) = x + ∫_0^x (2y0(t) + 1) dt
- Repeat the process using the new function as the initial guess: y2(x) = x + ∫_0^x (2y1(t) + 1) dt
- Continue the process until the successive approximations converge to a single function.
It’s important to note that the method of successive approximations is only one method to solve an integral equation, other methods such as the method of variations of parameters, the method of undetermined coefficients, or numerical methods may also be used.
It’s also important to know that the solution to an integral equation is not unique, it depends on the specific form of the integral equation and the initial or boundary conditions.
Partial differential equations
A Partial Differential Equation (PDE) is an equation involving an unknown function of several variables and its partial derivatives concerning those variables. These equations express the relationship between the partial derivatives of a function and the function itself. PDEs are used to model a wide range of physical systems, including heat conduction, fluid flow, and electromagnetic systems.
Example: u_t = u_xx + sin(πx)
A partial differential equation (PDE) is an equation that involves the partial derivatives of a function concerning two or more independent variables. In this example, u is the unknown function, t and x are the independent variables, and u_t and u_xx represent the partial derivatives of u concerning t and x respectively.
One method to solve this PDE is by using the method of separation of variables. This method involves assuming that the solution can be written as a product of functions of t and x, and then solving for each of these functions separately.
Solution:
- Assume that the solution can be written as u(x,t) = X(x)T(t)
- Substitute this ansatz into the PDE and divide by X(x)T(t)
- X(x)T'(t) = X”(x)T(t) + sin(πx)T(t)
- Dividing by T(t) X(x) and T(t)X”(x) respectively, we get the following ordinary differential equations:
a. X(x)T'(t) = X”(x)T(t)
b. T(t)X(x) = sin(πx)
- Solving the first equation, we get
a. T'(t) = λT(t)
b. λ = X”(x)/X(x)
- Solving the second equation, we get
a. X(x) = Acos(πx) + Bsin(πx)
b. A, B are arbitrary constants
- Since λ is a constant, we can solve the equation for T(t)
a. T(t) = Ce^(λt)
b. C is an arbitrary constant
- Thus the general solution of this PDE is
u(x,t) = (Acos(πx) + Bsin(πx))*e^(λt)
It’s important to note that this is only one way to solve a partial differential equation and depending on the complexity of the equation and the initial or boundary
Systems of equations
Two or more equations have to be solved simultaneously. They can be linear, non-linear, or a combination of both.
These are some examples of types of equations that are commonly encountered in algebra, but many others exist. It’s also worth noting that equations can be transformed and manipulated to fit into different categories, for example, a polynomial equation of degree 3 can also be a cubic equation.
Here is an example of a system of equations where one is linear and the other is non-linear:
Example:
2x + 3y = 6
x^2 + y^2 = 4
A system of equations is a set of equations that involve multiple variables. In this example, x and y are the variables, and we need to find the values of x and y that make both equations true. The first equation is linear because it is a first-degree equation in x and y and the second equation is non-linear because it has a power of 2 on x and y
One method to solve this system of equations is by using substitution or elimination.
Solution:
- We can solve for x in the first equation by isolating it:
x = (6 – 3y)/2 = 3 – (3/2)y
- Substitute this expression for x into the second equation:
(3 – (3/2)y)^2 + y^2 = 4
- Solve this equation for y:
y = ±√(4 – (3 – (3/2)y)^2)
y = ±√(4 – (9/4)y^2 + (9/2)y – 9)
- We can simplify the equation and we get
y^2 – 2y – 1 = 0
y = (2 ± √2)/2
- Substitute this value of y back into the first equation to find x:
x = 3 – (3/2)y
So the solution of this system of equations is (x,y) = (3-3/2(2+√2)/2 , (2+√2)/2) and (x,y) = (3-3/2(2-√2)/2, (2-√2)/2)
It’s important to note that this is only one way to solve a system of equations and depending on the complexity of the equations and the initial or boundary conditions other methods such as the Newton-Raphson method, or graphing the equation can also be used.
It’s also important to note that a system of equations can have different types of solutions such as no solution, unique solution, or infinitely many solutions, the solution depends on the nature of the equations involved and the coefficients of the variables.
Type of Equations used in Power System Engineering
Load flow analysis and optimization algorithms are used in power systems engineering to determine the steady-state voltage and current conditions in a power system. The types of equations used in these methods can vary depending on the specific algorithm or technique being used, but they generally involve a combination of linear and non-linear equations.
- Linear equations: Linear equations are often used in load flow analysis to represent the complex relationships between power system variables, such as voltage, current, and power. These equations take the form of linear equations, that can be written as Ax = B, where A is a matrix of coefficients, x is a vector of variables, and B is a vector of constants.
- Non-linear equations: Non-linear equations are also used in load flow analysis, particularly in methods that model the behavior of components such as generators, transformers, and transmission lines. These equations can be represented as f(x) = 0, where x represents the variables and f(x) is a non-linear function of the variables.
- Differential and algebraic equations: Some load flow analysis techniques involve solving a set of differential and algebraic equations (DAE) that represent the dynamic behavior of a power system. This type of equation has partial derivatives concerning time.
- Optimization algorithms: Many optimization algorithms such as Gradient Descent, Conjugate Gradient, Newton’s Method, etc.. are used to determine the optimal solution to the system of equations in load flow analysis and power system optimization problems. These algorithms use different types of mathematical optimization techniques and equations to find the optimal solution to the system of equations.
It’s important to note that load flow analysis and optimization algorithms can be different depending on the specific method or algorithm used, also the types of equations used will depend on the method being applied, and can vary depending on the specific application and the details of the power system being modeled.
Gauss-Seidel, Fast Decoupled, Jacobi, and Backward/Forward Sweep in Power System Analysis
Gauss-Seidel, Fast Decoupled, Jacobi, and Backward/Forward Sweep are all methods used to solve a system of non-linear equations that are commonly used in power systems analysis. These methods use a combination of linear and non-linear equations to model the behavior of a power system and determine the steady-state voltage and current conditions.
- Gauss-Seidel method: The Gauss-Seidel method is an iterative method that is used to solve a system of non-linear equations. It uses a combination of linear equations to represent the relationships between the variables in the system and an iterative process to approximate the solution.
- Fast Decoupled method: Fast Decoupled method is an improvement over the Gauss-Seidel method. It is also an iterative method that uses linear equations to represent the relationships between the variables in the system and an iterative process to approximate the solution. It is more efficient than Gauss-Seidel.
- Jacobi method: The Jacobi method is another iterative method that is used to solve a system of non-linear equations. Like Gauss-Seidel and Fast Decoupled method, the Jacobi method uses a combination of linear equations to represent the relationships between the variables in the system, and an iterative process to approximate the solution.
- Backward/Forward Sweep method: This method also known as the Gauss-Seidel Load Flow method is also an iterative method that uses a combination of linear equations to represent the relationships between the variables in the system and an iterative process to approximate the solution. However, it uses a different iterative process, called a backward-forward sweep process.
All these methods are used to solve a set of non-linear equations that represent the power system, they differ in the specific implementation and the way the equations are being solved. It’s also important to note that the method being chosen depends on the specific scenario, such as accuracy, computational cost, and the specific power system being modeled.
Getting Started with MATLAB and Implement Different Algebra Equations
Getting started with MATLAB involves installing the software and familiarizing yourself with its interface and tools. Once you have MATLAB installed, you can begin to explore its capabilities by working through some examples and experimenting with different types of equations.
Linear algebra is a branch of mathematics that deals with vectors and matrices and their operations. MATLAB has a variety of built-in functions and commands for working with linear algebra problems. Here is an example of how to implement linear algebra in MATLAB:
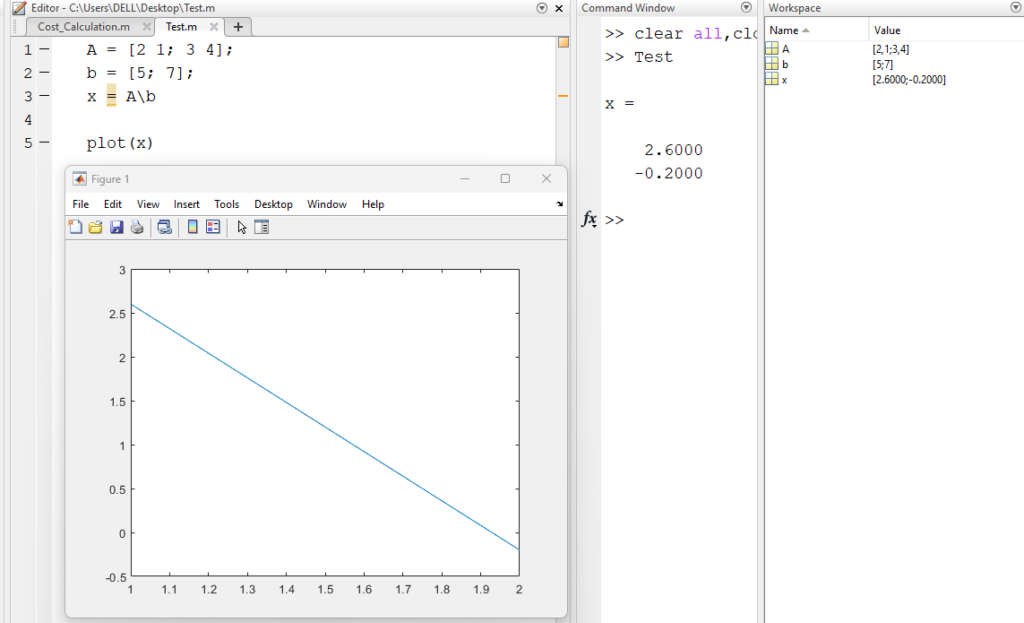
Example: Solve the system of linear equations given by the matrix equation Ax = b, where
A = [2 1; 3 4], b = [5; 7], and x = [x1; x2]
Start by defining matrices A and b in MATLAB. You can do this by using the square brackets [] to create matrices.
A = [2 1; 3 4];
b = [5; 7];Now, use the left division operator ” to solve the equation Ax=b. The left division operator is used to solve a system of linear equations in the form of A\b = x, where A is a coefficient matrix, b is a constant matrix, and x is a variable matrix
x = A\b
- The output will be the values of x1 and x2 that solve the system of linear equations.
x =
-1.0000
2.0000It’s important to note that this is just a basic example, and you can use MATLAB for more complex linear algebra problems as well. For example, you can use the eig function to find the eigenvalues and eigenvectors of a matrix, the svd function to perform singular value decomposition, or the lu function to factor a matrix into lower and upper triangular matrices.
Online MATLAB Homework Help Service
Our simulation tutor is offering services related to online MATLAB homework help. We provide comprehensive and personalized assistance to students looking to improve their understanding and proficiency in the use of MATLAB for solving mathematical and engineering problems. Whether you’re working on a specific assignment or need help with a broader concept, our team of experts is here to provide the guidance you need to succeed.
Our MATLAB homework help service includes one-on-one tutoring sessions, where students can receive personalized attention and guidance from experienced tutors. We also offer online resources such as video tutorials, sample codes, and practice problems to help students learn and review key concepts.
Our tutors are highly qualified and experienced in the use of MATLAB, and can help students with a wide range of topics, including linear algebra, optimization, differential equations, and data visualization. They will walk you through the problem-solving process, explaining the concepts and techniques needed to solve the problems and answering any questions you may have.
In addition to providing help with MATLAB homework, our tutors can also help students prepare for exams, offering review sessions and test-taking strategies. We also offer help with other simulation software such as Simulink, DlgSILENT, etc.
If you’re looking for a reliable and effective online MATLAB homework help service, our simulation tutor is here to help. Contact us today to schedule a tutoring session or to learn more about our services.
Conclusion
Understanding algebraic equations is an essential skill for anyone in the fields of science, mathematics, and invention. Algebraic equations are used to model physical phenomena, generate new ideas, and solve complex problems. With MATLAB’s powerful tools such as the left division operator “”, eig function or svd function functions one can easily solve a system of linear equations with ease. Our online MATLAB homework help service provides comprehensive support to students who need assistance understanding the basics or tackling more complex concepts related to algebraic equations. We offer one-on-one tutoring sessions as well as video tutorials and practice problems so that you have all of the resources needed to succeed. So if you’re looking for reliable help with your algebraic equation assignments or exams, contact us today!
MATLAB is a powerful software for solving mathematical and engineering problems, but it can be challenging to get started with. Fortunately, our online MATLAB homework help service provides comprehensive support to students who need assistance understanding the basics or tackling more complex concepts. Our experienced tutors are knowledgeable in linear algebra, optimization, differential equations, data visualization, and other topics related to MATLAB programming. We offer one-on-one tutoring sessions as well as video tutorials and practice problems so that you have all of the resources needed to succeed. If you’re looking for reliable help with your MATLAB assignments or exams, contact us today!
